Ever thought about chess ratings? The highest chess rating ever for a human is held by Magnus Carlsen at 2882. The lowest is shared by many people at 100. The United States Chess Federation initially aimed for an average club player to have a rating of 1500. There is no theoretical highest or lowest possible Elo rating (the best computers are at ~3500 and the negative ratings are theoretically possible, but those people will get kicked from tournaments, so they arbitrarily set 100 as a lowest possible rating).
This particular range of numbers from 100 – 3500 is a consequence of the base and divisor that Arpad Elo chose. The Elo rating system for chess uses a base of 10 and a divisor of 400. Why? According to wikipedia the 400 was chosen because Elo wanted a 200 rating point difference to mean that the stronger player would win about 75% of the time, and people assume that he used 10 as a base because we live in a base 10 world. Interestingly if he would have used base 9 then 200 points would exactly be a 75% chance of win, where base 10 is more like 76% :
1 /(1+9(200/400)) = .25
1 /(1+10(200/400)) ≈ .2402
But enough on Chess. I like the playoffPredictor mathematical formula that puts the teams between roughly 0 and 1 instead of 100 and 3500. But what base and divisor do I use with that system?
Last year I went with base equal to the week number (1-17) and a divisor of .4. The reason for the week number is because bases 2-3-4 don’t exponent out to crazy scenarios, so in week 2 when there is very little data it does not make such drastic judgements. The divisor I picked empirically, it seemed to fit the data and it was also a callout to Elo’s 400.
Really though I have been doing some fiddling and I think a base of 1000 and a divisor of 1 will work better. Here are some spreadsheet results.
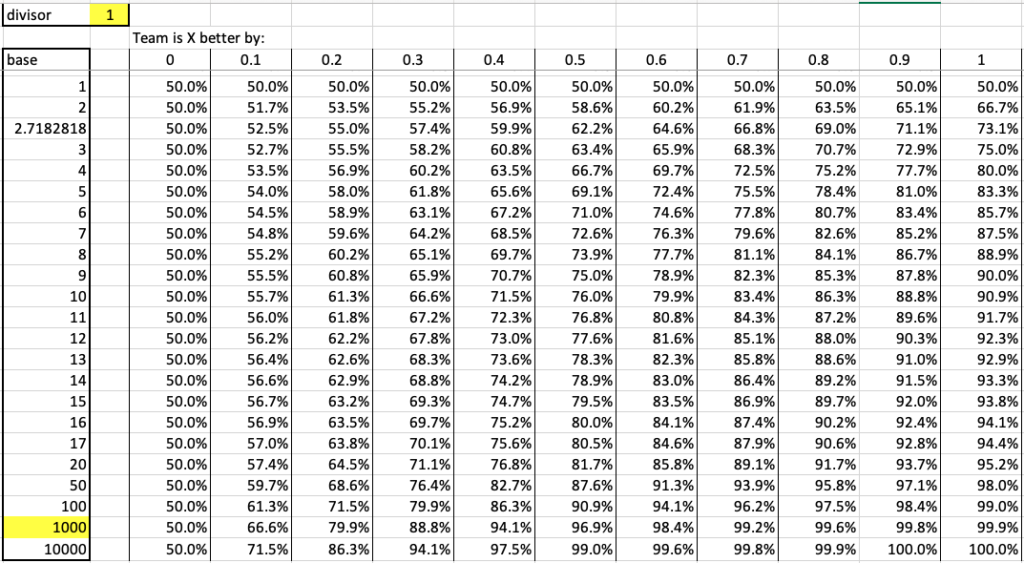
To read the above table, look at the row for 1000. This reads so if a team is better by .2 (like computer ratings of .9 and .7 for the 2 teams) then the .9 team as a 79.9% chance of winning. I need to model these against real life, but I feel this is a start.
Further for choosing a base and divisor the following are all equivalent pairs:
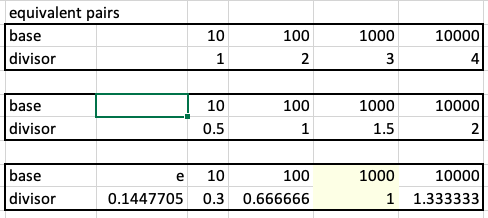
So 1000 and 1 give the same result as 10000 and 1.3333, or 100 and .6666. In the same way 1000 and 3 give the same result as 100 and 2, or 10 and 1. Log math.
So I’m going to move to a base of 1000 and a divisor of 1. The divisor of 1 make sense — take that out of the equation. Then, what base should you use? Empirically 1000 seems to fit well. I need to backtest with data from week 13-14 when ratings are pretty established to see how the percentages mesh with Vegas. To do.
At a base of 1000 and divisor of 1, a team with a rating +.16 more than an opponent will have a 75% chance of winning. So in this sense +.16 corresponds to 200 points in chess Elo.
In my rating the teams will be normally distributed with a mean at 0.5 and a standard deviation around 0.25. Meaning teams that are separated by 1 standard deviation, the better team has a 85% chance at success. For example, the following teams are all about 1 sigma apart:
- #1 Georgia (~1)
- #20 BYU (~.75)
- #70 Illinois (~.5)
- #108 Tulane (~.25)
- #129 1AA (FCS) (~0)
So Georgia has a 85% chance of beating BYU, BYU has a 85% chance of beating Illinois, Illinois has an 85% chance of beating Tulane, and Tulane has a 85% chance of beating a FCS school. Is that right? Not sure
Keeping with the logic, Georgia would have a 97% chance of beating Illinois [1/(1+1000^(-.5))]. BYU would have a 97% chance of beating Tulane. Are those right? I think so. Would need to check against Vegas.
tldr; PlayoffPredictor.com used to use week number and .4 for the base and divisor, but now uses 1000 for the base and 1 for the divisor.
