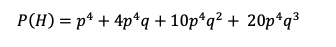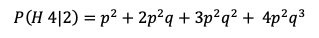This year I was fortunate enough to make one really good trade and hold a portion of it through fruition. Here I will document the trade and the way it has evolved over the course of this year.
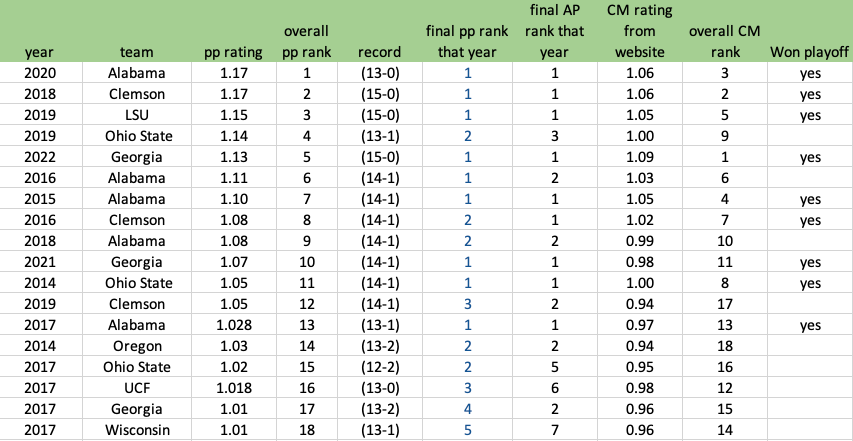
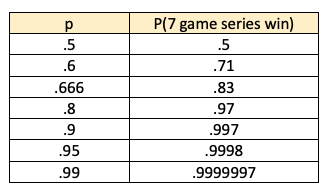
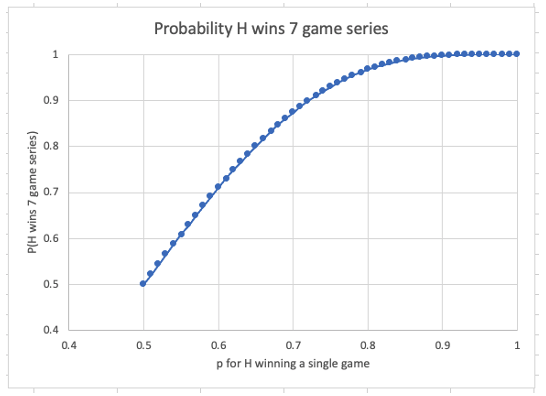
Towards the end of 2023 I shaped up what my 2024 portfolio would include. I like liquidating everything at the end of a calendar year and re-buying what I like and believe in. For 2024 I decided I would put 6% of my speculation portfolio into 3 options, 2% each which worked out to about $6,000 each option. The 3 equities I decided to buy options on were NVDA, RIVN, and QQQ. Here is the the setup in NVDA coming out of Jan-Dec 2023:

It had a great 2023, tripling from 150 to 500. Sometimes last year’s winners are also this year’s winners — look at DELL and EMC in the late 90s.

And above is the entry trade into NVDA.
My reasoning for this trade was that I like this setup. I have been blow away by AI and ChatGPT and GitHub CoPilot. During the fall I spend a decent amount of time coding for my website and app for playoffPredictor.com. To say that AI made my coding so much better is a gross understatement. You simply can’t do this development on Intel processors – it has to be GPUs and NVIDIA. So there is my conviction. Also, look at the 2023 performance of NVIDIA. There is the huge gap up from 300 to 400 in May when they announced earnings, and then really ‘UNCH’ for the rest of the year. Well, I guess going from 400 to 480 is 20% which is far from 0%, but for a speculation stock this volatile that is growing earnings by 10X over last year- yeah 20% is pretty much unchanged. I like stories like that which are due for a total repricing, not just a change in price based on what you could have bought it for yesterday.
Here notice the date and the amount. Ideally I would have made this trade on 1/2, but instead it is on 1/9. Sometimes I get nervous on these trades and just want the price to fall a bit further. If I would have made this trade on 1/2 and done $6,000 – the price was 50 cents, so I would have bought 120 contracts instead of 30. Hmm…. @#%#$^#%&. Oh well can’t live in the past. And there is no way I would have thrown $6k at such a nonsense idea. I mean 50% in 10 weeks on a $1 trillion company is nuts.
To speak to that nuts, planning my trades in December I never wanted NVDA at 750 strike and 3/15 expiration. I actually was planning on 600 strike and 4/19 expiration. But the problem was it was just too expensive. On Jan 2 the 600 call for 4/19 was trading for $10. I waited the first week of January to pull the trigger and the price got down to $8, but that’s still too expensive for me. I like to buy options that are about 0.20 cents to 0.50 cents as a rule when I’m swinging for the fences. I was watching the price the first week of January and hoping to get a better price. But the price kept going up, and by Monday 1/9 the 600 calls were trading at $20. So I said what the hell and threw down $4,500 on 30 contracts at a much higher strike of 750 for about $1.50 each. I’d rather have 30 contracts instead of 5 contracts any day. My thinking is that you can get rich at 100+ contracts and just have a good return at <10 contracts. And it is a good thing I did not end up buying the 600 strikes. They would be worth ~ $300 each contract now which is 300/10 = 3000% A 30 bagger. Very good — but as it turns out not as good as the 750s
So here is what NVDA and the call has done 2024 year to date:


In a perfect world yes this was a .38 cents to 223 opportunity: 223/.38 = 58,600% or a 586 bagger! Imagine turning $2,000 into $1,000,000…
Well all January NVDA went up and the call went up, straight from $1.50 to $5 by the end of January, and then a quick run up from $5 to $25 in the first 3 trading days of February. Very nice I turned $5k into $15k and then suddenly from $15k to $75k was quite happy (ecstatic). I decided to celebrate by purchasing an Apple Vision Pro that came out on Feb 2. So I sold my first 2 calls on Feb 5th for $25 a contract ($5,000 credit, covered my initial investment. Everything else was now house money).

After February 5th it got much more interesting. Earnings were to be released Feb 20, and wall street was all abuzz with this earnings report. I felt it could go up into earnings, but I was playing with real money now. I’d never spend that kind of money on an out of the money option into earnings, but I didn’t have to spend that money — it just grew into that valuation.
My next move was on 2/12. By that time NVDA was trading at 720, getting really close to the 750 strike. Generally I sell an option when it goes from out of the money to at the money. This time I did not really want to sell, I wanted to see where this ride would go, so I decided to sell an upside call against my call position. Normally people sell upside calls against share ownership positions; it is called a synthetic dividend. But this was a little different. Essentially I turned by 750C into a 750/930 call spread. I sold 28 contracts at 930 strike for the same expiration of 3/15. My reasoning was that I was now guaranteed $20k of profit, even if NVDA tanked. Nice!

Of course I capped my upside at $180 per contract, but 180*28 is $500,000 – so I settled for a max profit of $500,000 with $20,000 guaranteed.
On 2/18 and 2/19 NVDA fell from 730 to 670. Earnings was on 2/20, and people wanted to lock in gains before earnings. That was somewhat painful. On paper each day I lost $30k or so. Basically all those gains to $75k gone, back to $20k total return. On earnings itself I did not watch at all. I texted my son an hour after close asking “Are we eating at the Ranch or at Taco Casa tomorrow”. His response “somewhere in-between”. My pulse quickened. After earnings it was back to $750 and I took the whole family to the Ranch for dinner the following evening. It was the feast of unrealized profits! Over the past 24 hours I had made $100k on paper. Other may be used to that, but I was not.

Now here is where I normally would sell the whole position. Earnings are done. The strike price has been met. It is too risky to risk everything and theta decay will kill you now. But I decided this time to just sell 8 contracts at effectively $31 each. And let’s see what happens with the other 20 contracts.

Now here is a trade I regret. From 2/23 to 2/28 NVDA drifted down from 820 to 775. Getting close back to the 750 strike I had a fit of paper hands and sold 5 more contracts on 2/29. I guess I just wanted to guarantee $60k in profits, so I sold.

The next trade was to buy back 2 of the 930 calls. from 3/1 – 3/4 (2 trading days; Friday and Monday) the price jumped from 800 to 880 and I suddenly realized taking out the 930 calls would be possible and then I’d be forced to sell. I just did not want to sell until expiration. I could have bought back all remaining 15 930 calls on 3/1 for $2k, but I didn’t and the price shot right back to the premium I collected in the first place.

Next I decided I wanted protection. I bought put options (expiring that Friday 3/8, 1 week before my call option expiration) so that I locked in $50 per contract no matter what. The only thing that could hurt me was if it closed Friday above 800 and then opened Monday below 800. I felt comfortable with that risk (it was trading 880 at that time). Sure enough these expired worthless, but that $760 spent helped me sleep at night.

Over 3/6 and 3/7 the price kept shooting up and was bumping right against 930. Well if I was still short the 930 I would have to sell, I mean at that point it is only risk with no reward as the 930 and 750 will both have a delta of 1. Only possibility is price goes below 930 and I lose more money on the 750s (still deep in the money) than the 930s (back to at the money). So I panicked and started buying back the 930 calls. Remember that $20k premium collected? Well, here was $12k just to buy them back. I was now long 15 contracts at 750 and short 6 contracts at 930.

Well on 3/8 open it broke through 950 and I sold 5 more contracts. I like to sell at market open, but I was on the Guardians of the Galaxy ride at EPCOT, so I had to finish that first. I sold the 5 contracts just outside the gift shop at 9:35am. I also bought back the last 930C contract. I kept thinking to myself the Guardians ride was tame compared to the NVDA ride. Why there is not a theme park with the whole theme of stock and options prices I have no idea — that is a wild ride! Total spread credit was $160 per contract.

On 3/12 I bought protection for 5 of the remaining 10 contracts for $4, financing it by selling upside calls at $1,000. I mean if I get $250 per contract I’m thrilled, and this guarantees a full $100 per contract. Of course both these expired worthless, except the insurance was nice this week as it drifted down on Thursday.

Thursday morning I went ahead and sold another 5 contracts at the open. Now I am locked into a minimum return for the whole trade. This trade is pretty similar to the 2/29 trade, done out of fear of loss or paper hands, same concept.

Friday morning is expiration day. Time to harvest what is left. But first I had to buy back the $1000 strike calls, else my account could be subject to infinite risk. Divorced from the big picture it was a good sale on its own – sold on Tuesday for $1,621 and bought back on Friday for $53. I guess if you think that way its a 30x return on your money in 2 days. Of course the catch is you have to tie up tens of thousands of dollars in shares or long options in order to make a trade where you sell premium in the first place. In a lot of ways it is not fair. $1,600 is a lot of money to most of the country and it is only accessible to people who already have means. I am sure someone reading this will be young and understand the concept, but be unable to execute it for themselves because they don’t have the money already, and that is a shame. I think Robinhood at least offers people money for loaning out their stock, even just a few dollars. That seems like a good start to me.


Finally, this morning I sold 3 contracts at open and in the afternoon at 2:45pm I sold the final 2 contracts. That open price ended up being the low of the day. Oh well. And I was going to buy that ivory backscratcher.
All totaled, it comes to $291,000 on a $4,500 investment, or a 6,500% gain, a 65 bagger. You only need a few of these in life to catch the options bug permanently. Do I wish I had held on the whole time, I mean it could be more like $600,000. While the answer is of course, I don’t think I would have had the mental energy to do this all the way to $600k. For that matter you could have bought the 950C expiring 3/15 for 0.05 cents on Jan 5th, and it would have been worth $50 on March 8 – a full 100,000% return – 1000x on your money. Turn $5k into $5M. You could have also done that with MSTR in February. I wish I would because houses on the beach are not cheap and I could use an extra 1 or 2 million if they are giving it away, but oh well. That kind of thinking is a trap. It is impossible to buy the low and to sell the high.
Here is one of the profit and loss bubble charts while it was trading at it’s high. Normally that percentage you are happy at 20% and 30%. The thing says %15,000. Just unreal.

Could I have done better? Yes, but. Common strategies that people use is to roll up (higher strikes) and potentially out (further calendar date) options as they go from out-of-the-money to at-the-money. If I would have done that and say harvested 50% each time while going up in 50$ chucks, I’ll bet I could have made a lot more money (I’ll have to compute that when I get back from Spring Break to see exactly how that would have worked out). But there is no way I could have done that, mentally. That would have meant selling $80,000 of options on 2/22 and then buying $40,000 that same day, like 3/15 800C. That would have been hard. I mean even though the money fungible and holding is the same as selling today and buying it tomorrow our human caveman brains can play with house money of $80k MUCH easier than playing with fresh $40k. I mean, I just would not throw that kind of money at an option expiring in 3 weeks. That’s irresponsible. People who can master that part of their psyche and not fall into that trap I am sure are fantastic options traders, but I have not conquered that hurdle yet.
Did I make mistakes? Yes. Here you have to separate true mistakes from just price anticipation, which is unknowable. Looking back at this I made 2 mistakes:
- On 2/29 when I sold the 5 contracts I should have also bought net new options at ~800 expiring 3/22. I should have used 10k of the 20k for that. That guarantees $50k on the trade, but you have to get longer on weakness if you believe in what you are doing, not just flatter.
- On 3/8 I should have sold everything. In my speculation account I have a rule – everything must be harvested 1 week before expiry. In my view options with less than a week is gambling and belongs in my timing account, not my speculation account. Now, of course that was the high that Friday morning, but that is irrelevant. I have to have the discipline that everything in the speculation portfolio must have an expiration >1 week out. This would mean that the protection I bought should also have been through 3/8, not 3/15. Unfortunately this was a $100,000 mistake (ouch)
In the end I think you need some conviction to stick with a trade like this. There is no way I would stick with it if I thought NVDA would not become larger than AAPL and MSFT, which I think it will this year. Now after that, it certainly can be cut in half. But if the thesis is that every single CPU in every computer and phone is dead in the AI world, yeah that is a big market. As for now, well it is spring break and I am headed to Mexico. Cashing out this week. No crazy options positions on vacation!